METROPOLIS2 Course

Session 1: Introduction

Lucas Javaudin

Spring 2024

Plan of this Session

  1. Course organization
  2. Overview of METROPOLIS2
  3. Getting started with METROPOLIS2
  4. Task for next session

Course Organization

Sessions

  1. Introduction (13th March)
  2. Supply side: road network (27th March)
  3. Demand side: agents, travel alternatives and trips
  4. Technical parameters and running the simulator
  5. Reading and understanding the results
  6. Case-study: Paris' low-emission zone (Input)
  7. Case-study: Paris' low-emission zone (Output)
  8. Extensions: fuel consumption, CO2 emissions and local pollutants

General Information

  • The session's slides are sent to all participants at the end of the session
  • One task wil be proposed at the end of each session (to be done for the next session)
  • Tasks are optional but highly recommended: Practice makes perfect
  • Any participant who completes all the tasks and writes a 2-page report can get an attendance certificate

Overview of METROPOLIS2

A Bit of History

  • 1997-2009: Simulator METROPOLIS1 [C++] (de Palma, Marchal, Nesterov)
  • 2001-2009: Interface for METROPOLIS1 [Java] (Marchal)
  • 2018-2021: Web interface for METROPOLIS1 [Python Django] (Javaudin)
  • 2021-: METROPOLIS2 [Rust] (de Palma, Javaudin)

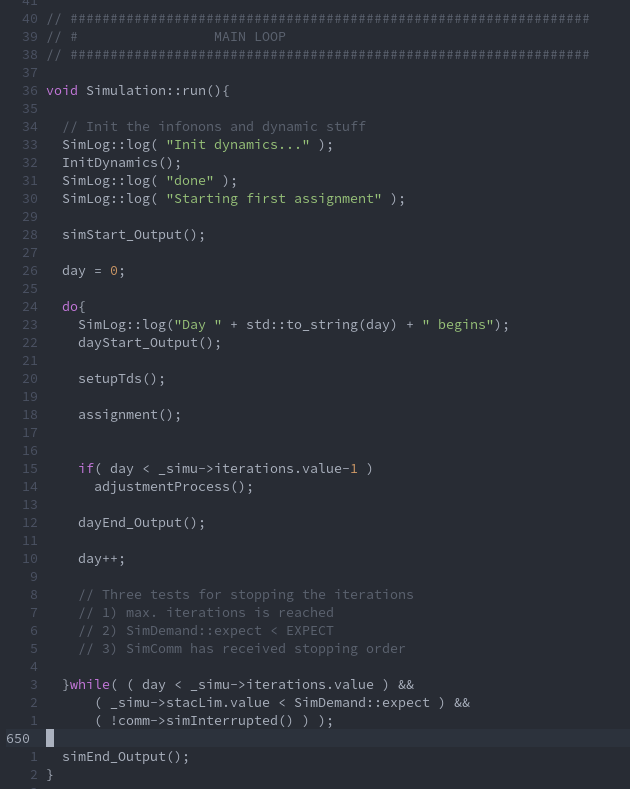
What is METROPOLIS2

Transport simulator with the following characteristics:

  • Agent-based
  • Multi-modal
  • Micro-founded
  • Dynamic
  • Adapted for small- and large-scale simulations
  • Fast
  • Extensible

General Flow

  1. Python scripts are used to convert data to the simulator's input files
  2. The METROPOLIS2 simulator reads the input files and writes output files (Parquet or CSV format)
  3. Python scripts are used to read the output files and produce results

Python scripts can be shared between users or replaced by other tools

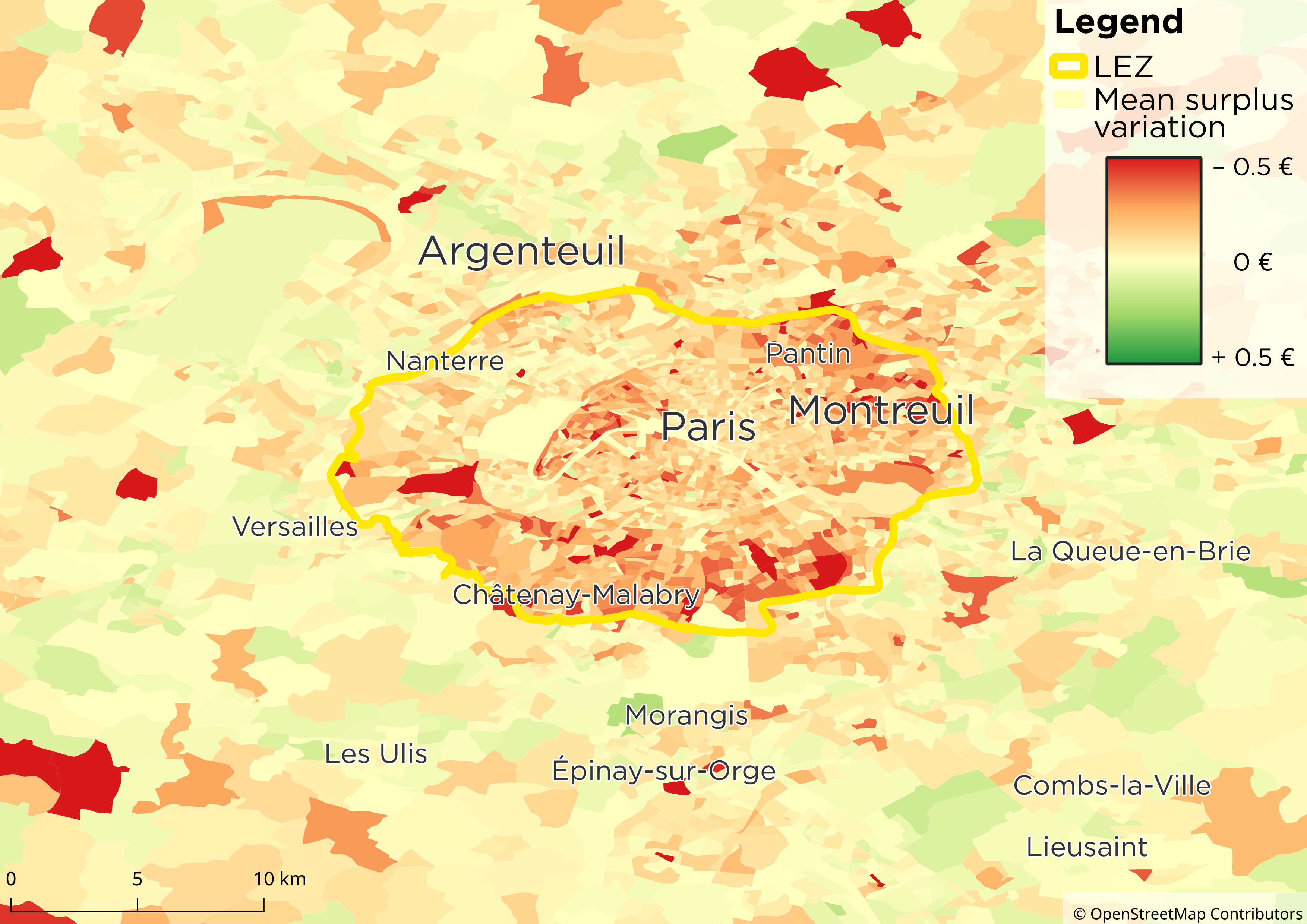
Examples of Productions

Travel surplus variation at the IRIS level when Paris's Low Emission Zone is implemented

Car flows for all trips going through highway A15 near Cergy

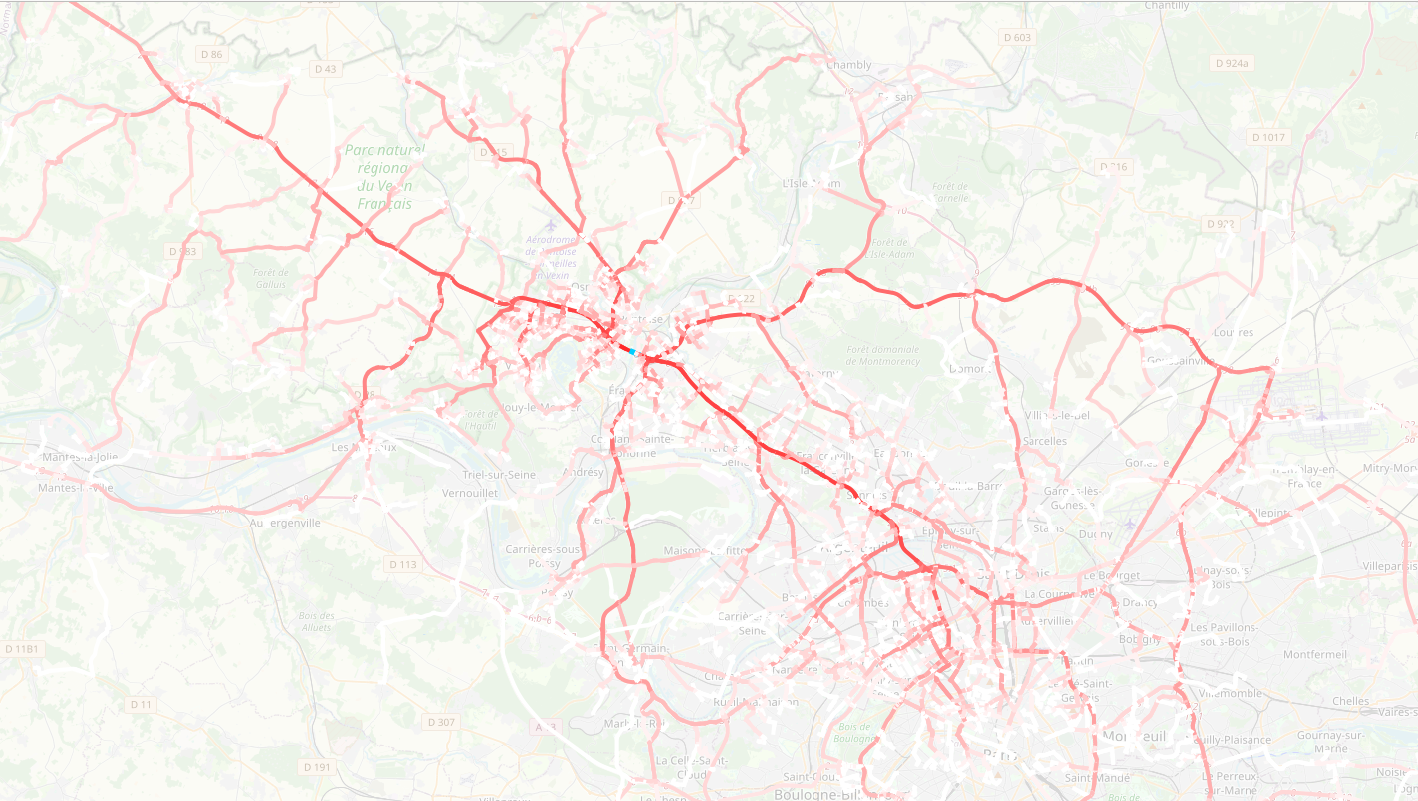
Public-transit flows by line, Paris' urban area, Morning peak

Vehicle movements in the surroundings of Cergy, 08:00 to 08:05

Comparison with METROPOLIS1

Improvements over METROPOLIS1:
  • Point-to-point trips (vs OD matrix)
  • Trip chaining
  • More flexible utility and choice models specifications
  • Full heterogeneity
  • Improvement congestion modeling
  • Different vehicle types (including speed limit and road restrictions)
Differences / regressions:
  • No en-route route choice
  • No proper toll implementation
  • No incidents

Comparison with METROPOLIS1

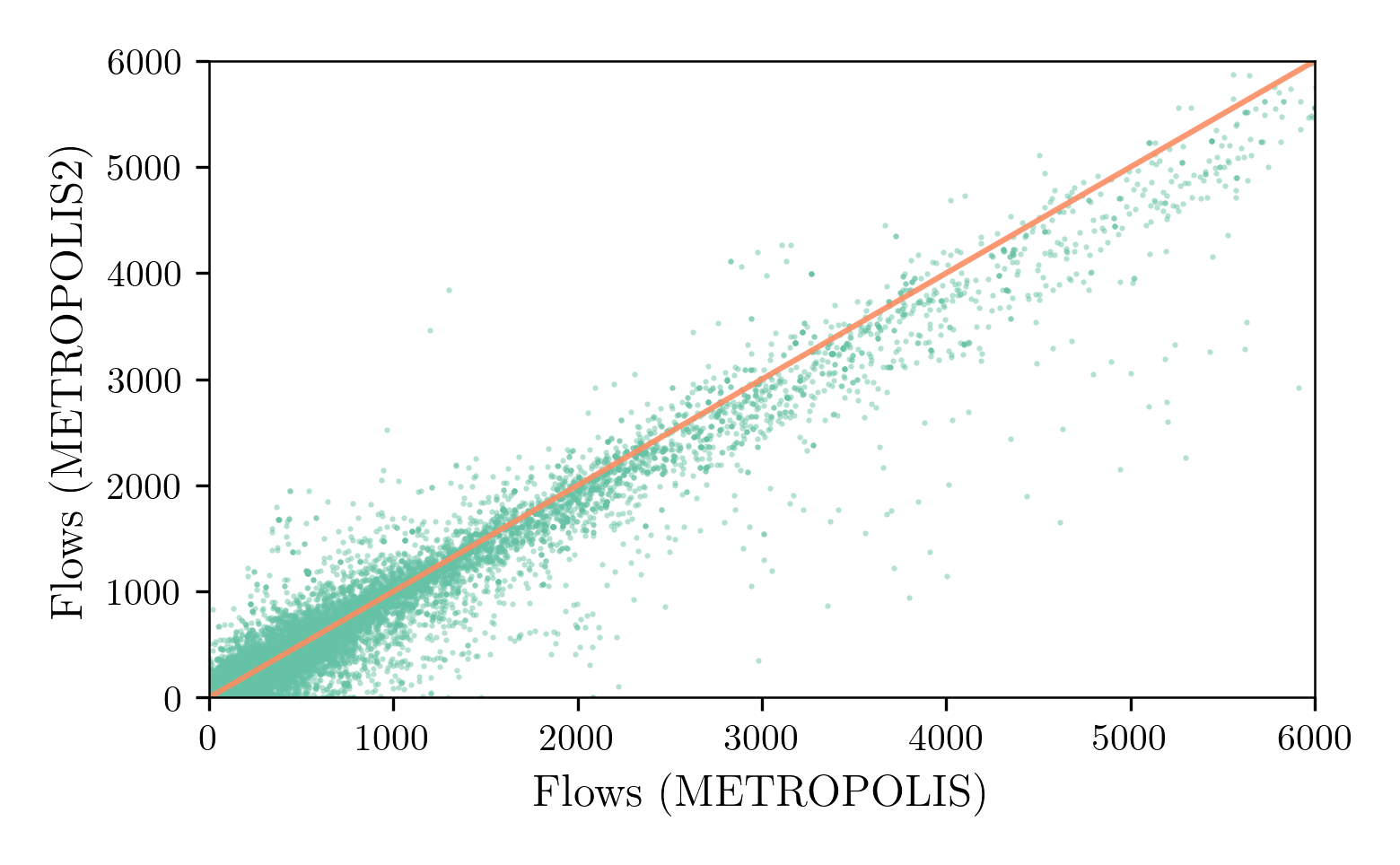
METROPOLIS2 replicates well the results of METROPOLIS1 for Île-de-France (convergence is better, running time is about 10 times smaller thanks to parallelization).

Comparison with MATSim

METROPOLIS2 MATSim
Trip-based Activity-based
Exogenous activity duration Endogenous activity duration
Flexible utility specification Charypar-Nagel utility function
CSV / Parquet input XML input
Discrete-choice theory Co-evolutionary algorithm
  • Discrete-choice theory: choice among all alternatives, based on discrete-choice models (e.g., Logit)
  • Co-evolutionary algorithm: choice in a limited subset of alternatives

Example: Simulating the Bottleneck Model

The Bottleneck Model

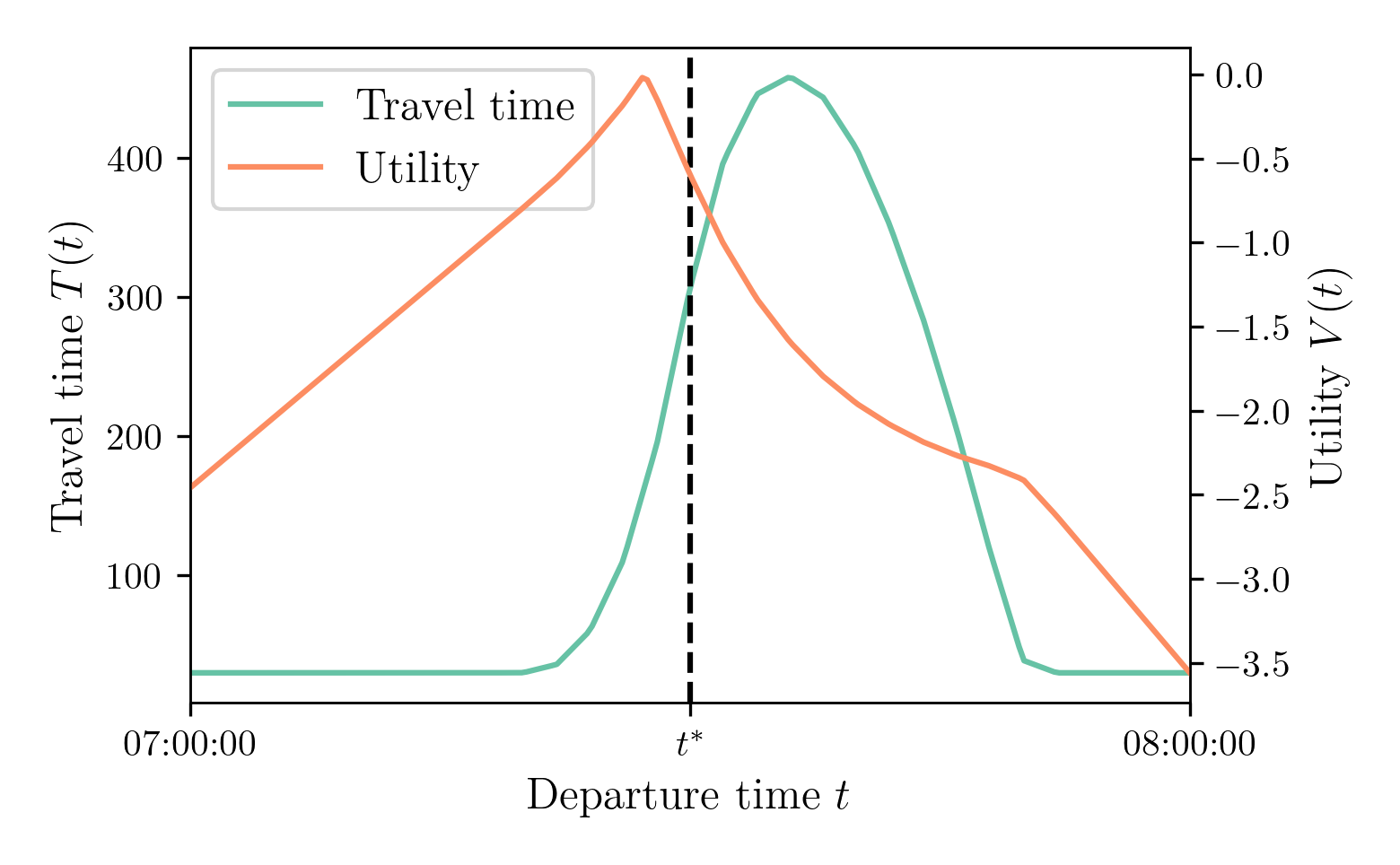
  • A road is connecting an origin $A$ to a destination $B$: free-flow travel time is $t^f$ and there is a point-bottleneck of capacity $s$
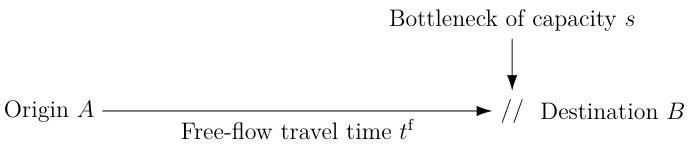
  • Travel time from $A$ to $B$ is \[ t^f + \frac{Q(t + t^f)}{s} \] with $Q$ the length of the bottleneck queue at time $t$.

The Bottleneck Model

  • $N$ agents are traveling from Origin $A$ to Destination $B$
  • Utility is given by \[ V(t) = -\alpha \cdot T(t) - \beta \cdot [t^* - t - T(t)]_+ - \gamma \cdot [t + T(t) - t^*]_+ \]
  • Agents choose the departure time maximizing utility (Arnott, de Palma and Lindsey, 1990): \[ t^d = \arg \max V(t) \]
  • Agents choose departure time $t$ with probability (Continuous Logit, de Palma, Ben-Akiva, Lefevre and Litinas, 1983): \[ p(t) = \frac{e^{V(t) / \mu}}{\int_{t^0}^{t^1} e^{V(\tau)/\mu} d \tau} \]

METROPOLIS2 Fundamental Flow Diagram

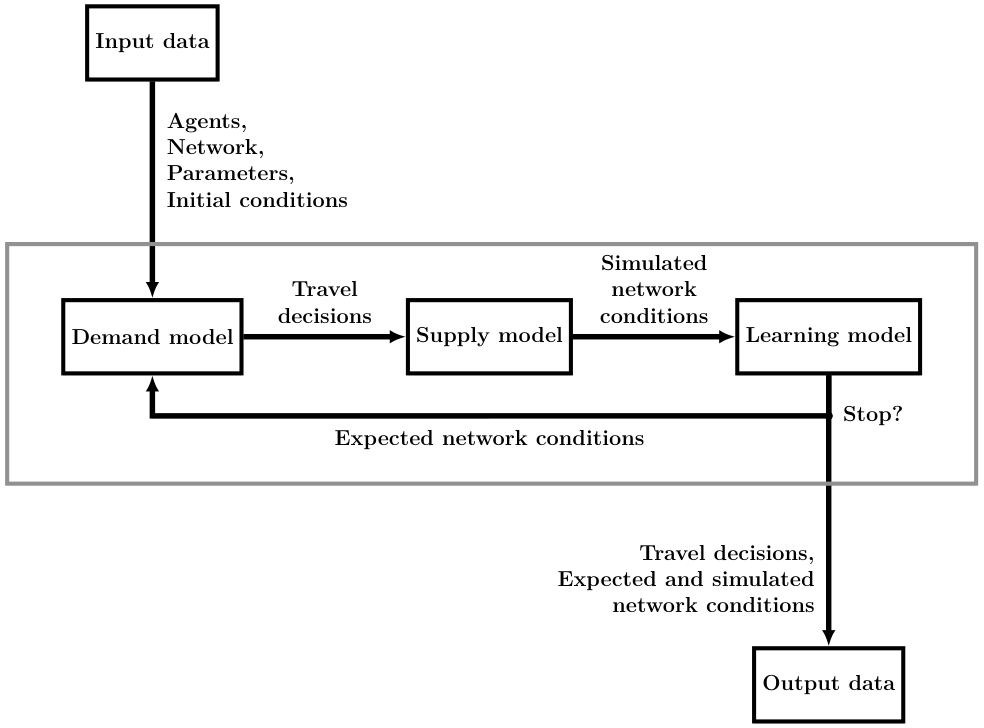
Input Data

  • Population: $N = 100,000$ agents, $\alpha$-$\beta$-$\gamma$ preferences ($\alpha = 10\$ / h$, $\beta = \gamma = 5\$ / h$, $t^*$ = 7:30 a.m.)
  • Road network: Single road, free-flow travel time $t^f$ = 30 seconds, bottleneck of capacity $s = 150,000$ cars / h
  • Initial network conditions: free flow

METROPOLIS2 Fundamental Flow Diagram

Demand Model: Computing Utility

We start from constant free-flow travel-time function and compute the utility function \[ V(t) = -\alpha \cdot T(t) - \beta \cdot [t^* - t - T(t)]_+ - \gamma \cdot [t + T(t) - t^*]_+ \]

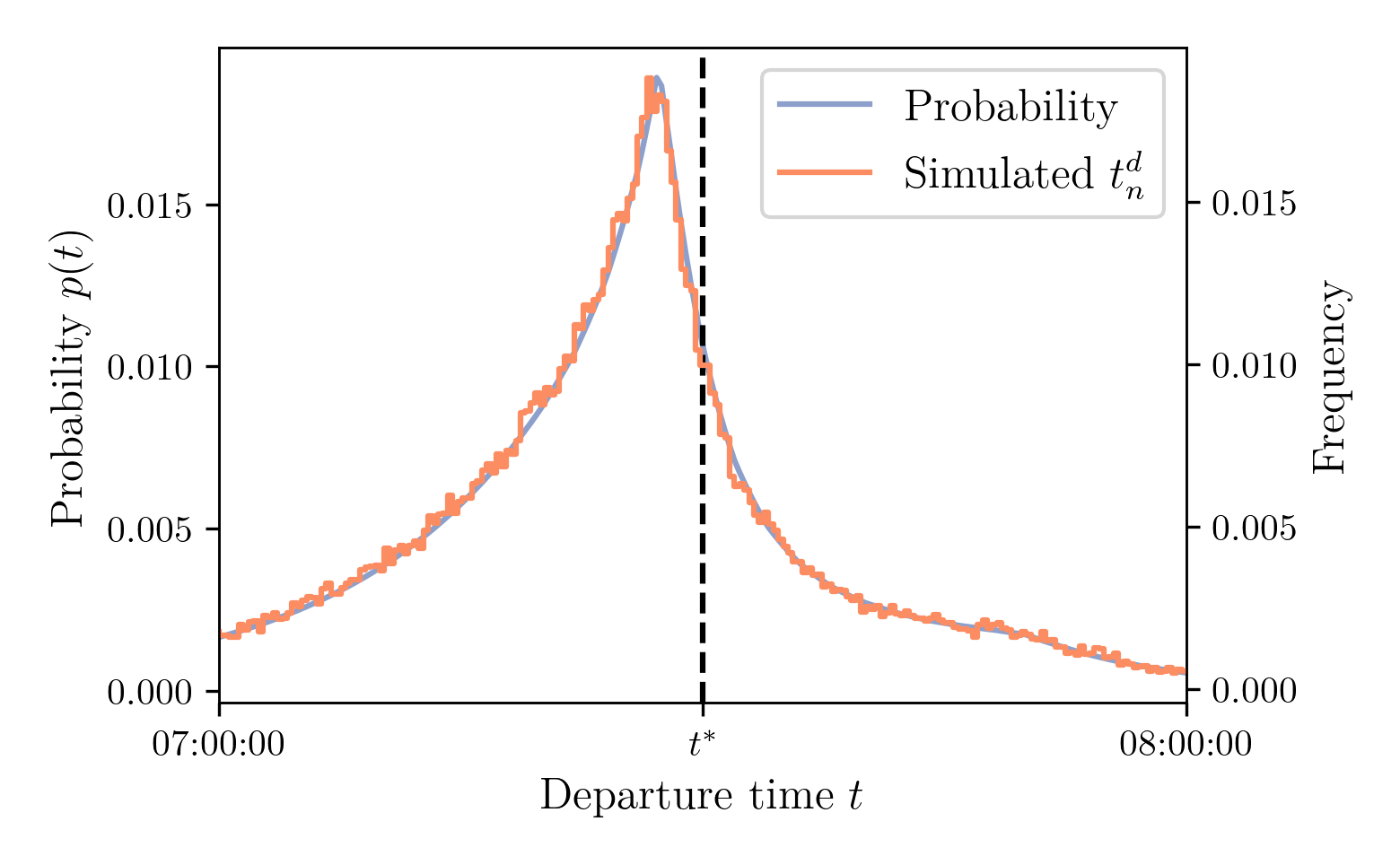
Demand Model: Computing Departure-Time Probability

The departure-time probabilities are computed from the Continuous Logit formula \[ p(t) = \frac{e^{V(t) / \mu}}{\int_{t^0}^{t^1} e^{V(\tau)/\mu} d \tau} \]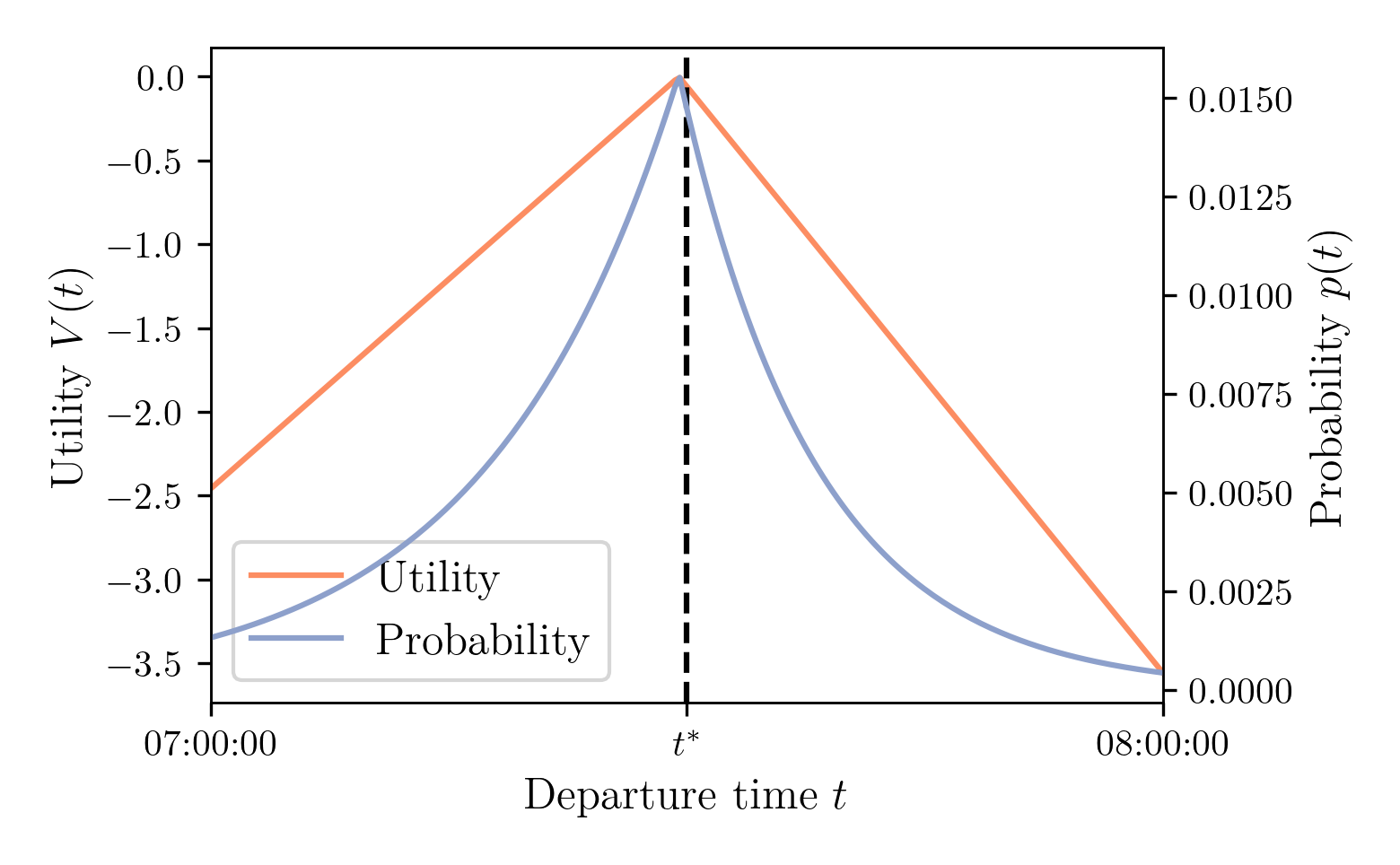

Demand Model: Simulating Departure Times

How to draw departure times from the probability function?

Inverse transform sampling: $t^d = F^{-1}(u)$ with $u \sim \mathcal{U}([0, 1])$ and $F^{-1}$ the CDF

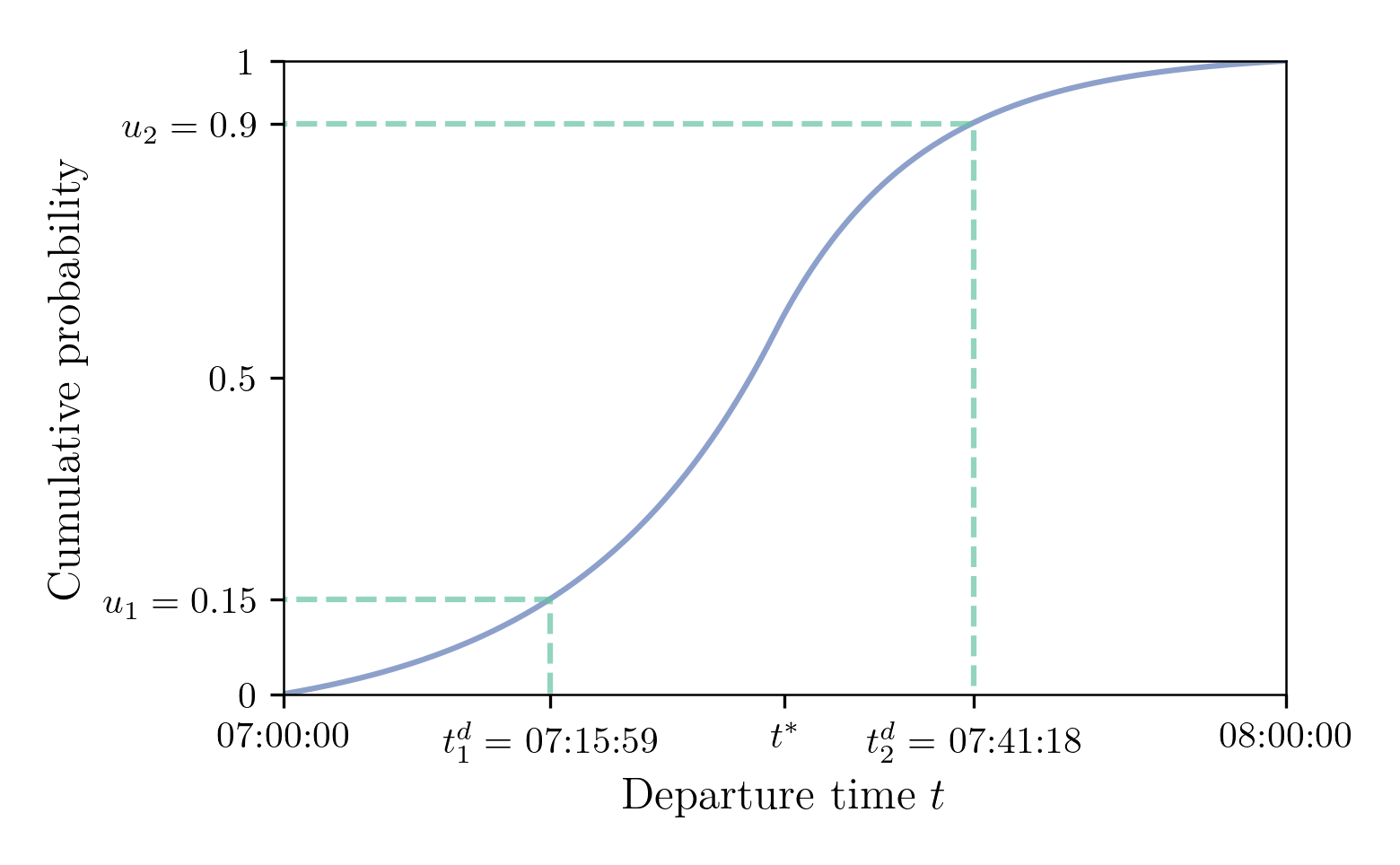
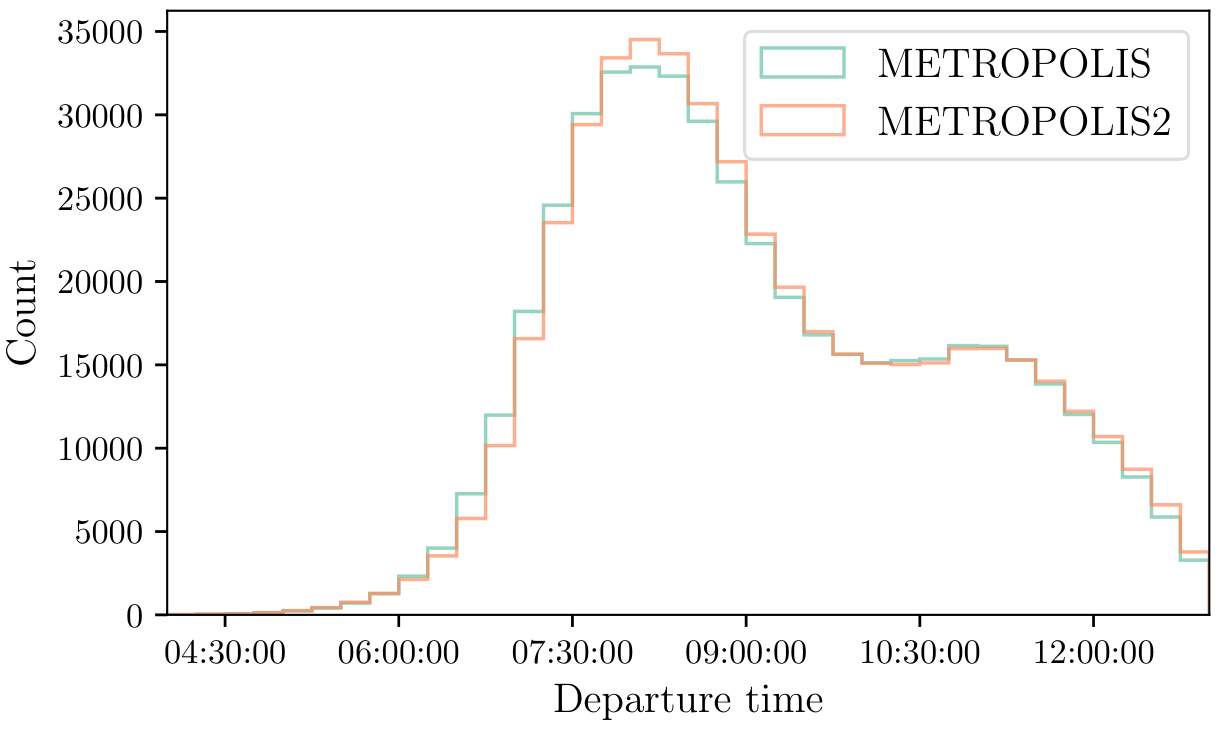
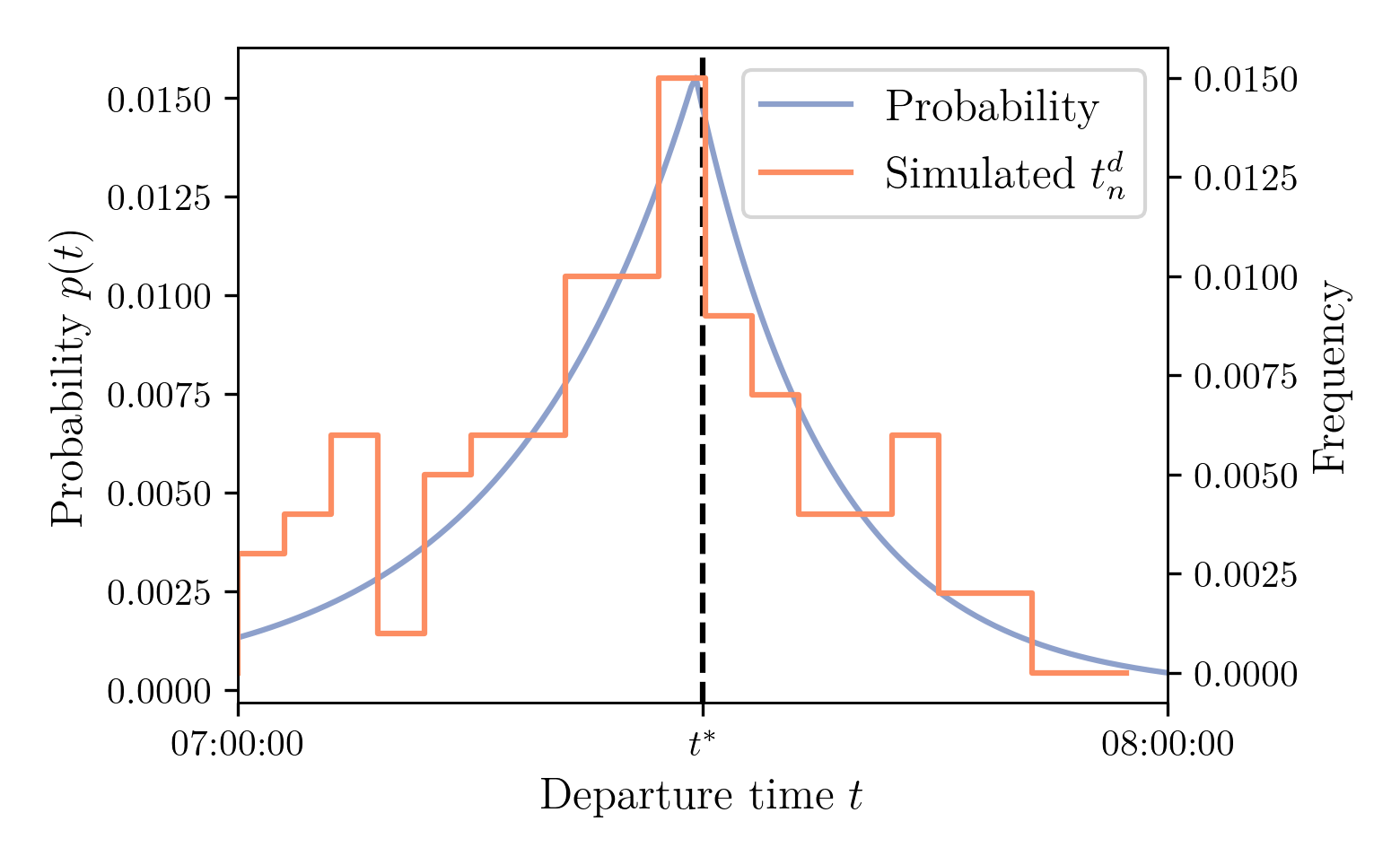
Demand Model: Simulated Departure Time Distribution

Draws with $N = 100$

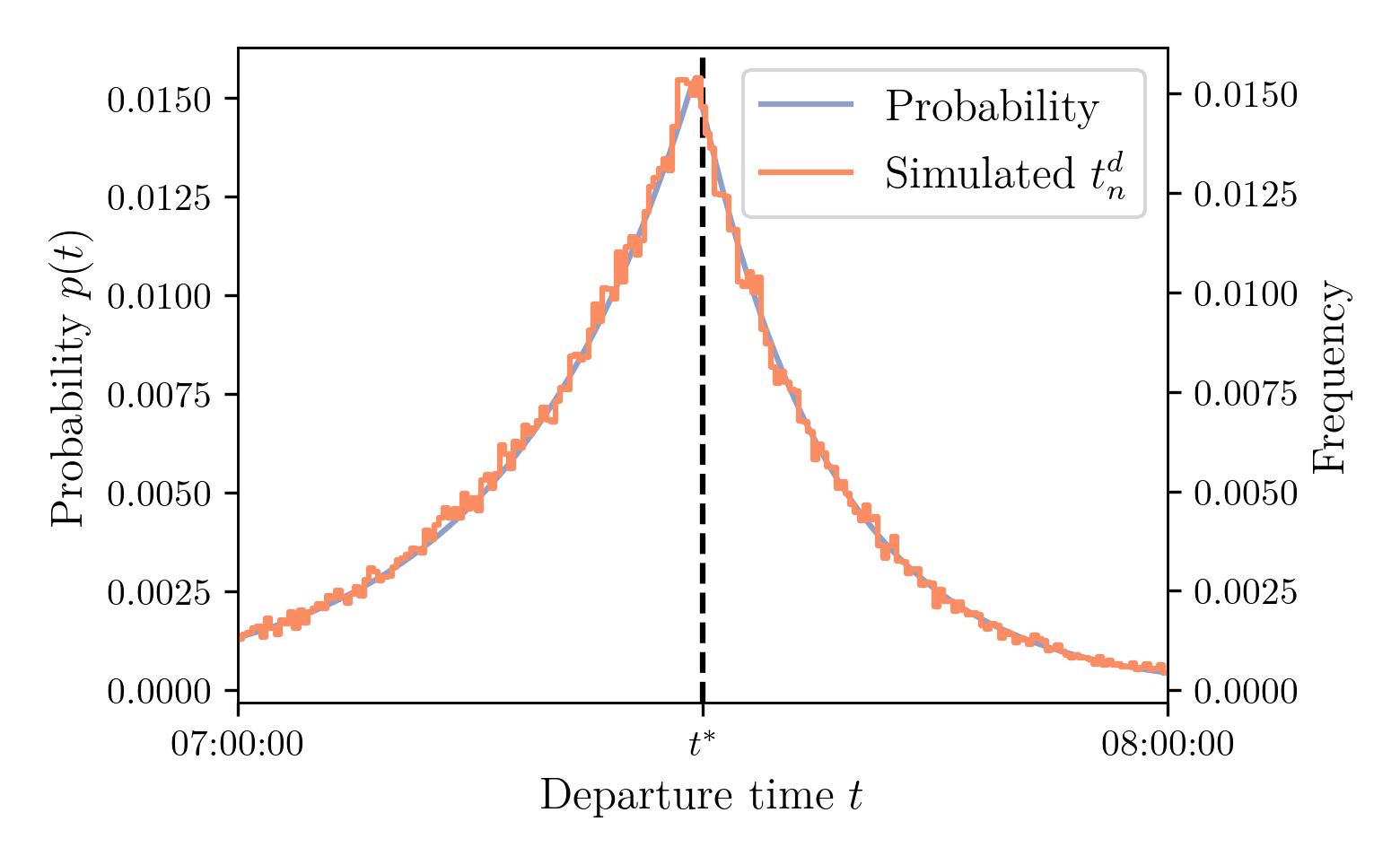
Demand Model: Simulated Departure Time Distribution

Draws with $N = 100,000$

METROPOLIS2 Fundamental Flow Diagram

Supply Model: Simulating Bottlenecks

  • Bottleneck capacity: \[ \text{900 cars / hour} \Leftrightarrow \text{0.25 car / second} \Leftrightarrow \text{4 seconds / car} \]
  • Departure times: $[1, 6, 7, 9]$
Events:
  • T1: Agent 1 enters the bottleneck, leaves immediately, bottleneck closed until T5
  • T5: Bottleneck opens
  • T6: Agent 2 enters the bottleneck, leaves immediately, bottleneck closed until T10
  • T7: Agent 3 enters the bottleneck, pushed to the queue
  • T9: Agent 4 enters the bottleneck, pushed to the queue
  • T10: Bottleneck opens, agents 3 leaves, bottleneck closed until T14
  • T14: Bottleneck opens, agents 4 leaves, bottleneck closed until T18
  • T18: Bottleneck opens
Arrival times: $[1, 6, 10, 14]$

Supply Model: Bottleneck Properties

  • Bounded by the capacity: The outflow of the bottleneck cannot exceed its capacity
  • FIFO: The cars exit the bottleneck in the same order that they entered it
  • Continuous time: It can work with very small or very large capacities

Supply Model: Simulated Departure and Arrival Time Distributions

$N = 100,000$, Capacity 150,000 cars / hour or 41.67 cars / second or 0.024 second / car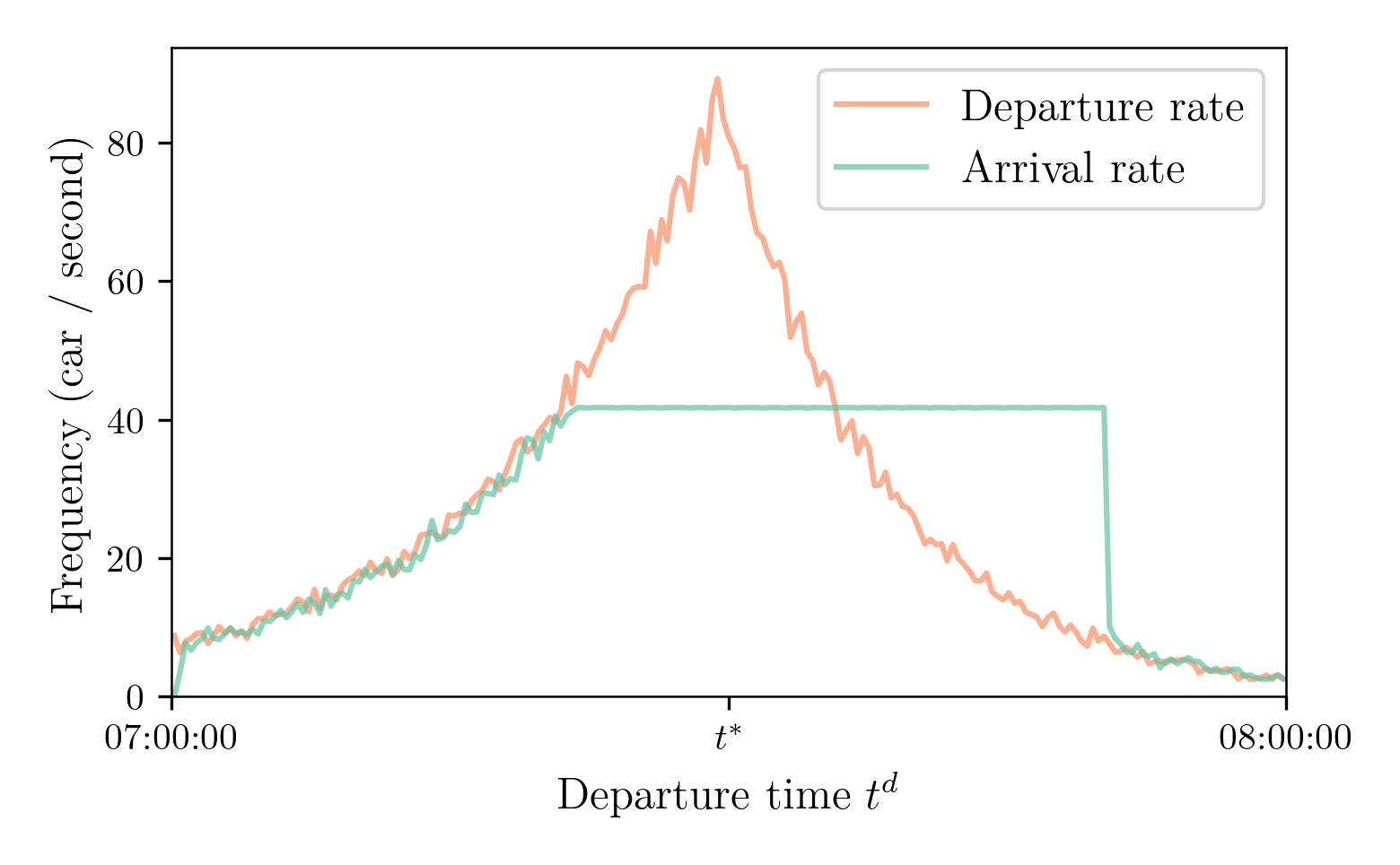

Supply Model: Simulated Travel Times

$N = 100,000$, Capacity 150,000 cars / hour or 41.67 cars / second or 0.024 second / car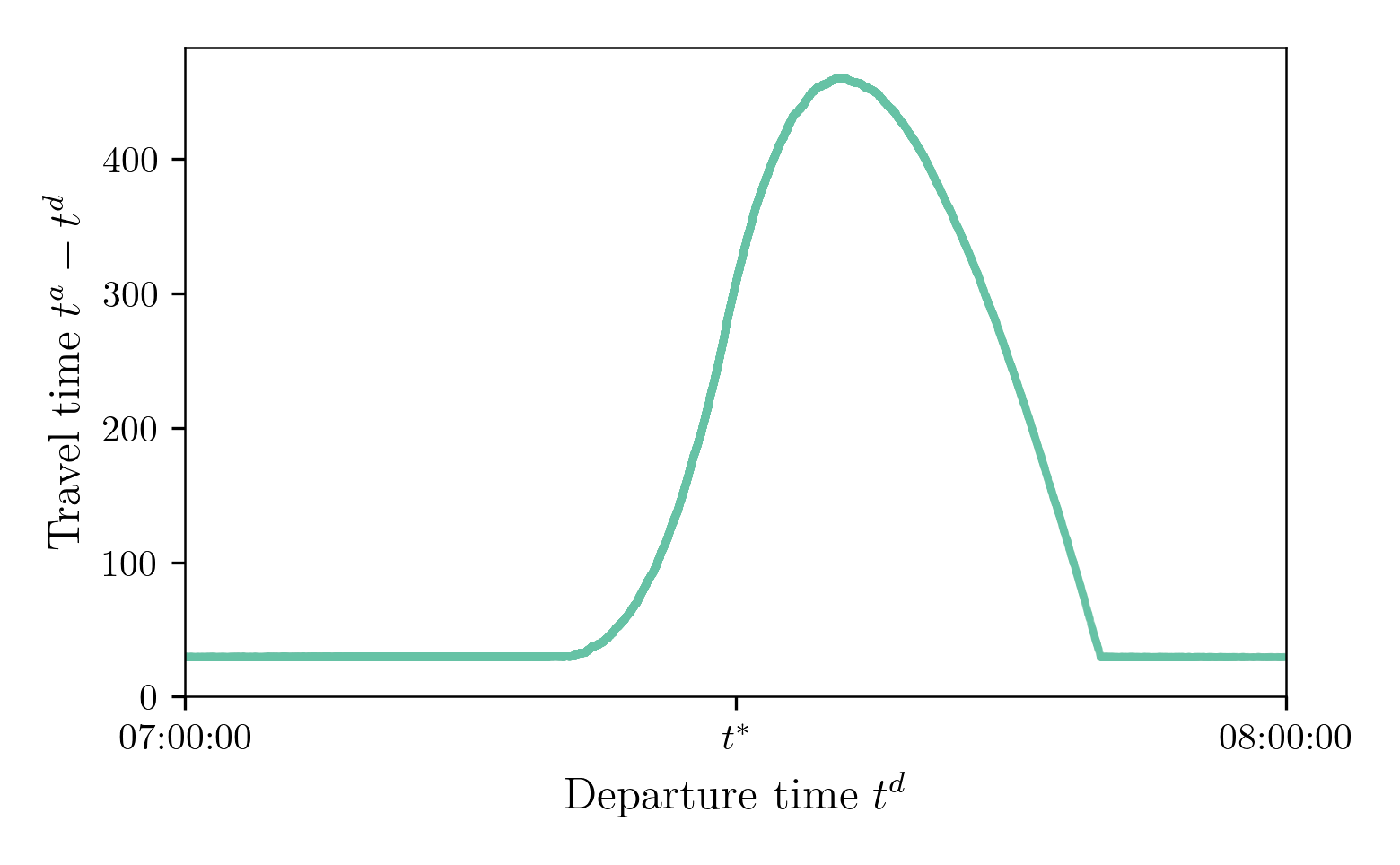

Supply Model: Simulated Travel Times

$N = 100$, Capacity 150 cars / hour or 0.04167 cars / second or 24 seconds / car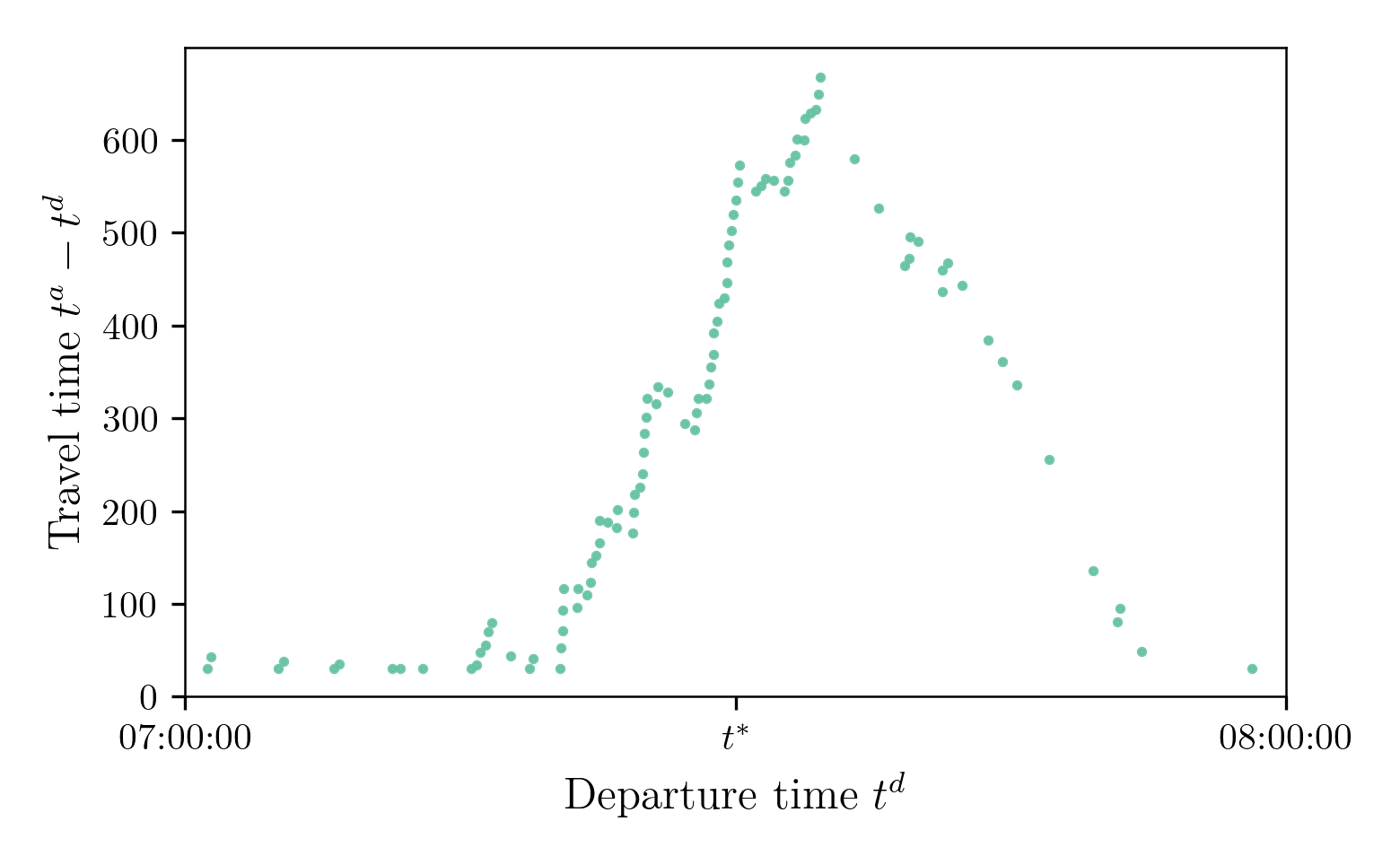

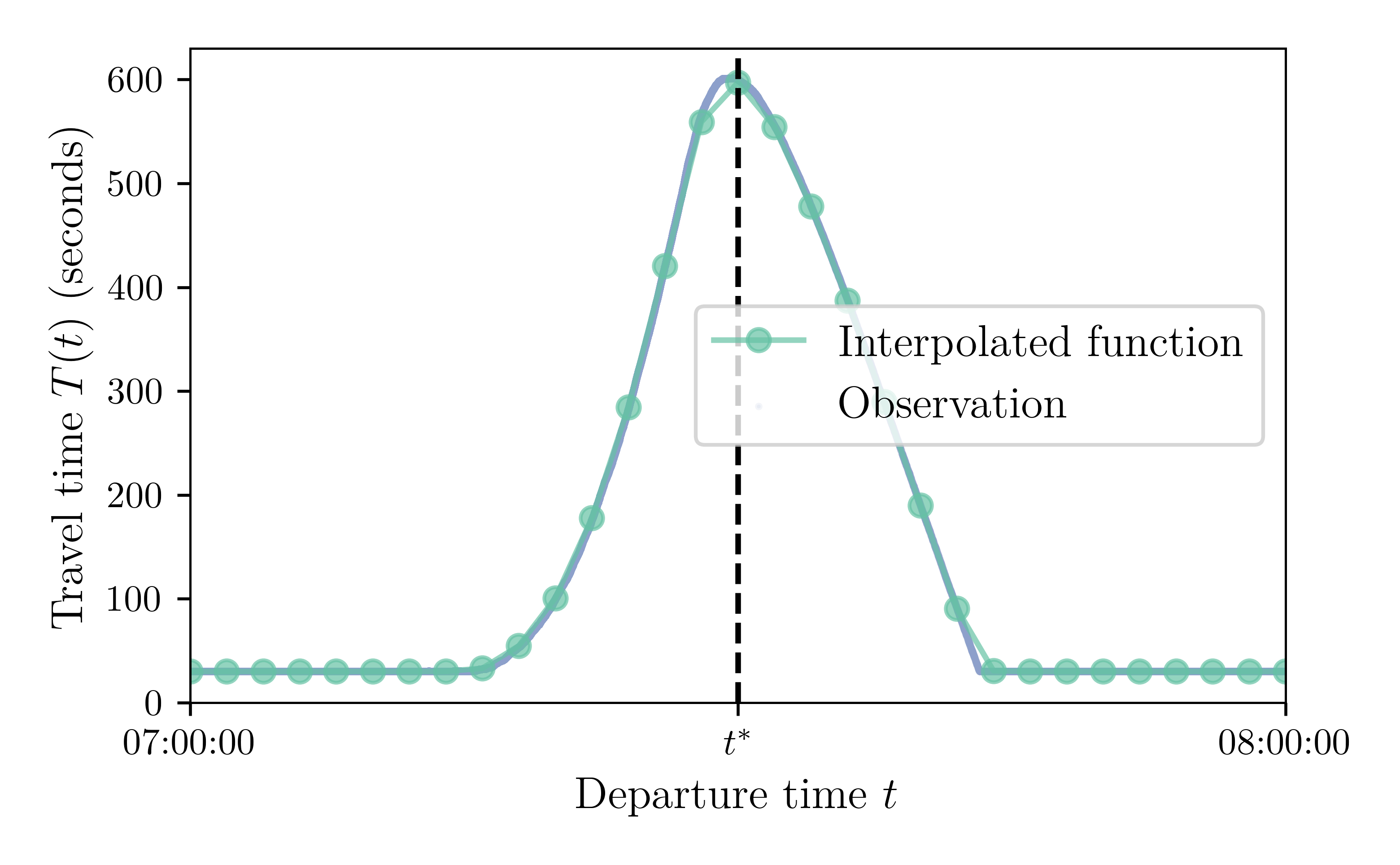
Supply Model: Piecewise-Linear Travel-Time Function

How to build the travel-time function from the simulated points? Linear interpolation!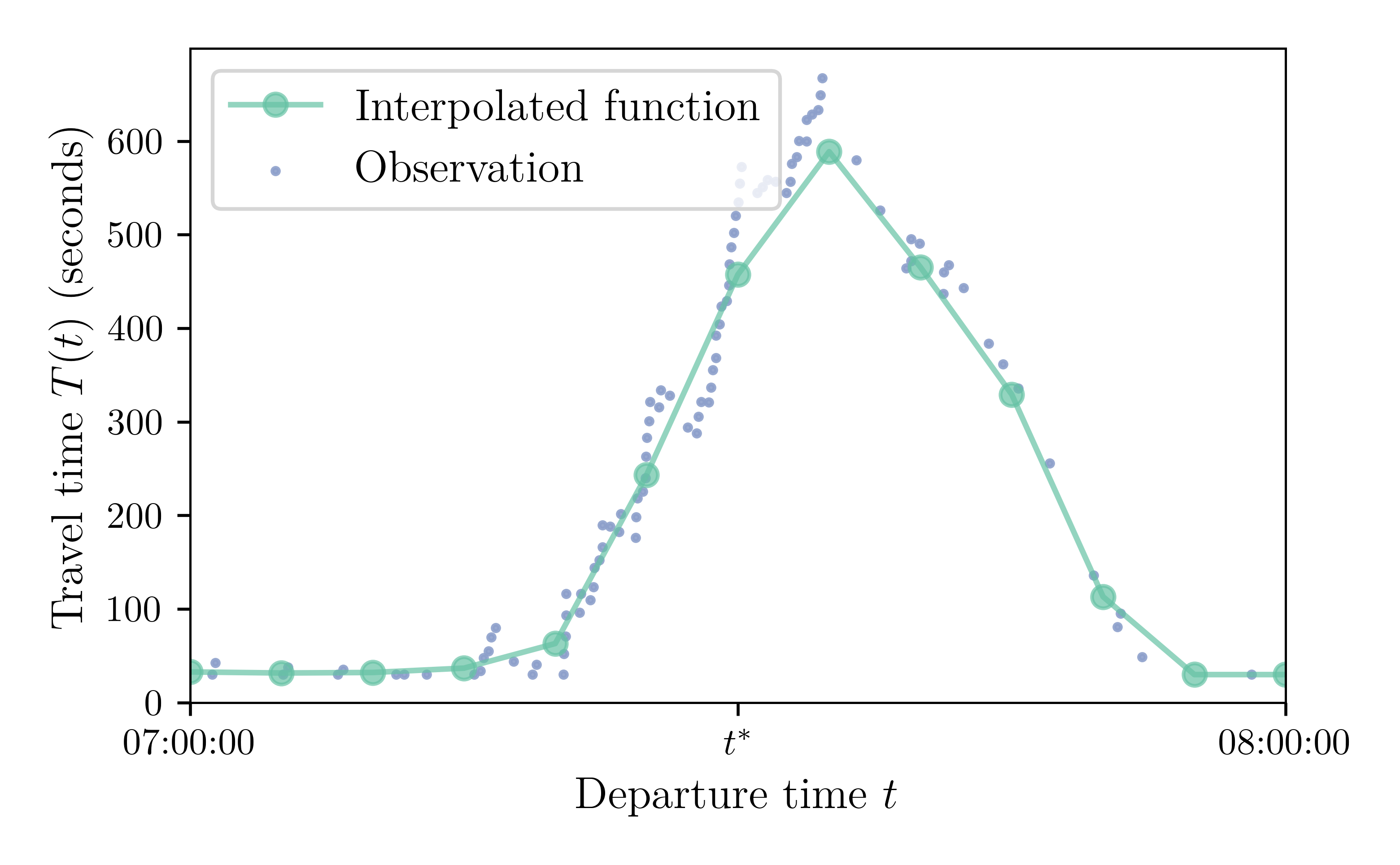
$N = 100$, Capacity 150 cars / hour or 0.04167 cars / second or 24 seconds / car

Supply Model: Piecewise-Linear Travel-Time Function

5-minute breakpoints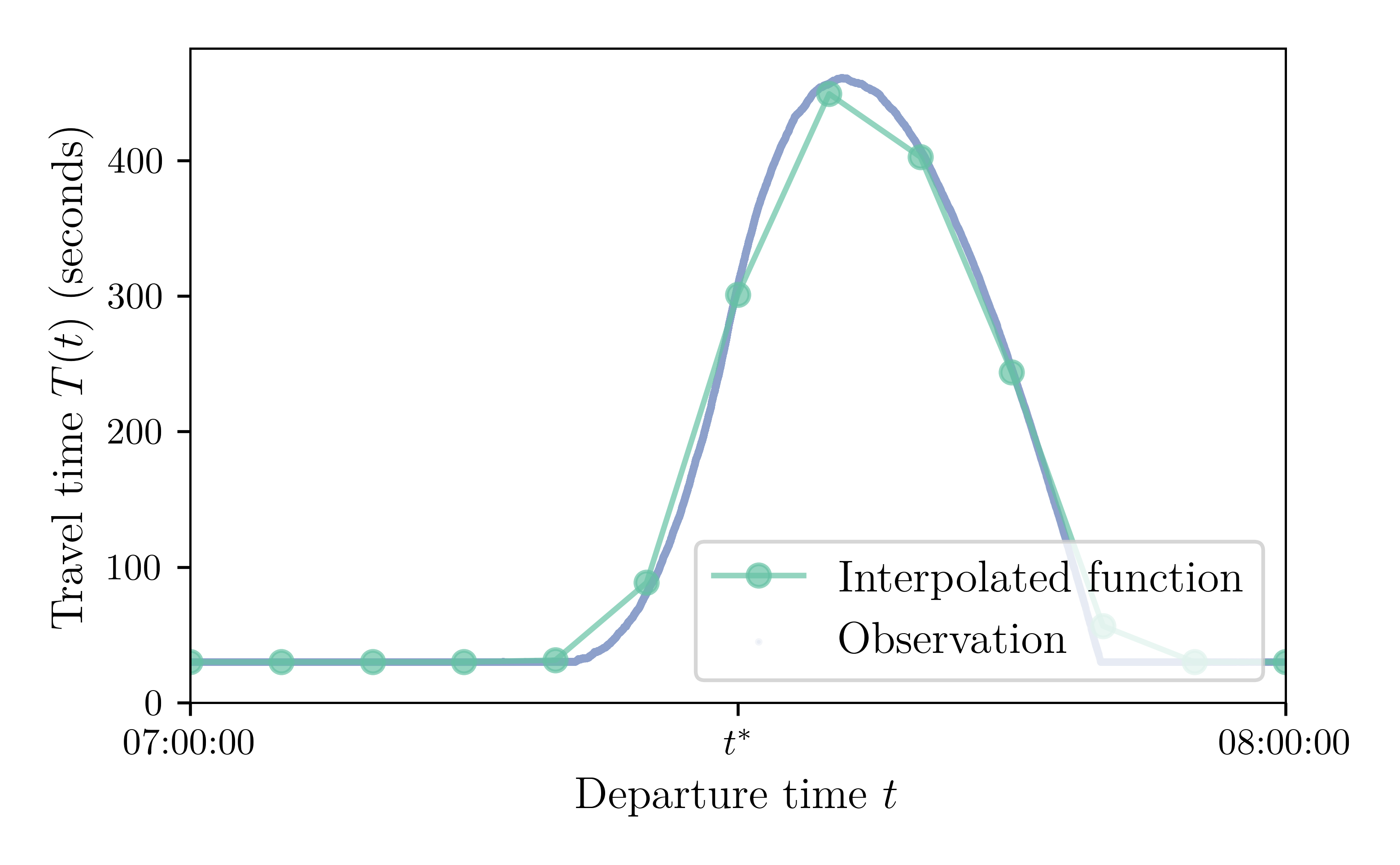

$N = 100,000$, Capacity 150,000 cars / hour or 41.67 cars / second or 0.024 second / car

Supply Model: Piecewise-Linear Travel-Time Function

2-minute breakpoints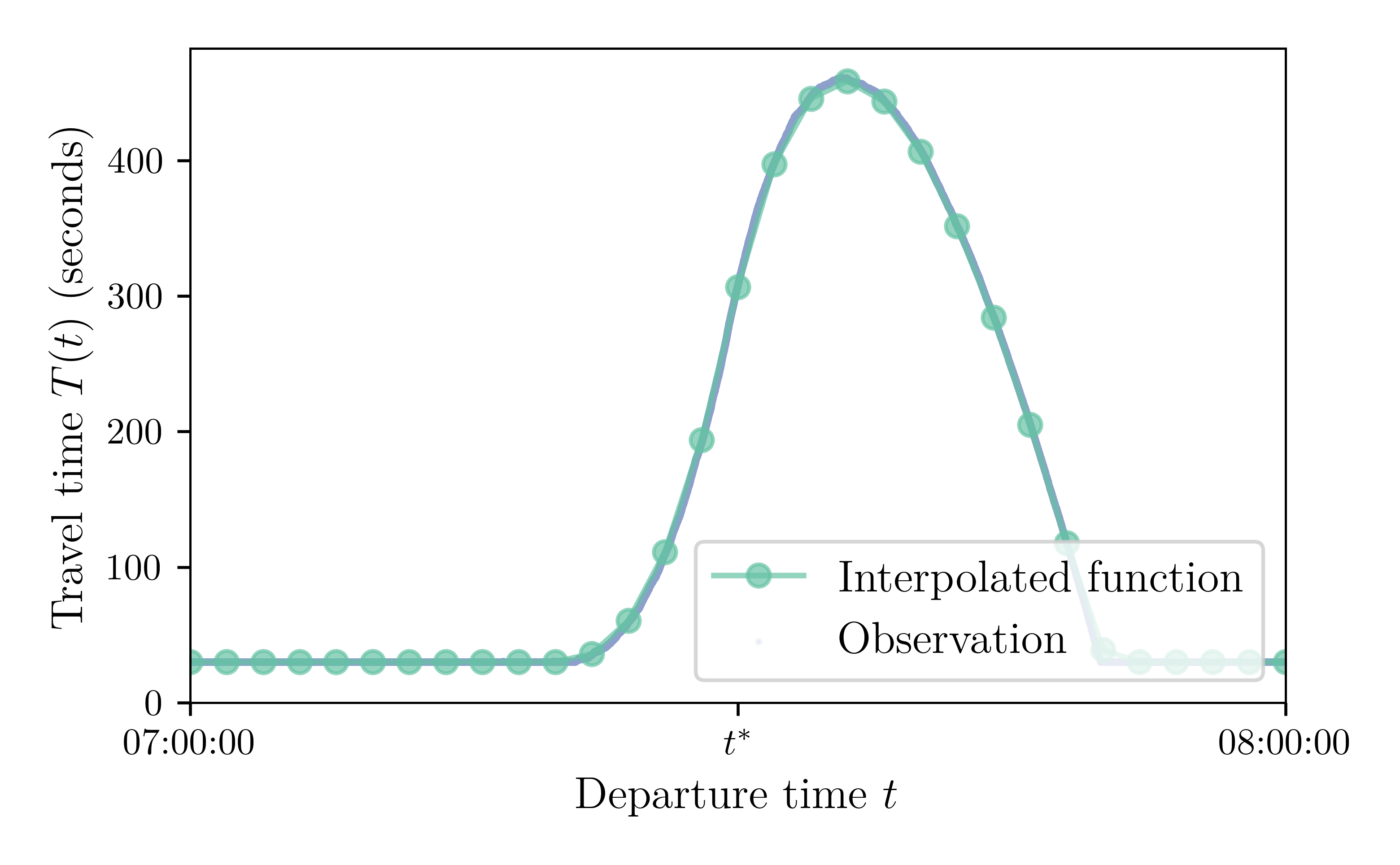

$N = 100,000$, Capacity 150,000 cars / hour or 41.67 cars / second or 0.024 second / car

Summary

Start from free-flow travel-time function
Draw the chosen departure times (demand model)
Simulate congestion and compute the resulting travel-time function (supply model)

Inconsistency / Non-equilibrium: The travel-time function used to simulate the departure times (in the demand model) does not match the travel-time function resulting from these departure times (in the supply model)

Nash equilibrium definition: No agent can increasing their utility by choosing another departure time, given the other agents' departure times

"Naive" METROPOLIS2

(TTF = travel-time function)

  • $\hat{T}$: Expected TTF, used to compute utilities in the demand model

  • $T$: Simulated TTF computed in the supply model from the chosen departure times

Naive algorithm:

  1. Initialization: $\hat{T} =$ free-flow TTF
  2. Demand model: Draw the departure times given $\hat{T}$
  3. Supply model: Compute $T$ resulting from the departure times
  4. If $T = \hat{T}$, stop.
    Otherwise, $\hat{T} \leftarrow T$ and go back to Step 2.

Second Iteration

Start from the previously simulated travel-time function
Draw the chosen departure times (demand model)
Simulate congestion and compute the resulting travel-time function (supply model)
Still not at an equilibrium

100 Iterations

METROPOLIS2 Fundamental Flow Diagram

Learning Model

  • The TTF expected for the next iteration depends on the TTF just simulated, $T$, but also on the previously expected TTF $\hat{T}$.
  • At iteration $\kappa$: \[ \hat{T}_{\kappa + 1} = f(\kappa, T_{\kappa}, \hat{T}_{\kappa}) \]
  • Exponential smoothing method: \[ f(\kappa, T_\kappa, \hat{T}_{\kappa}) = \lambda T_\kappa + (1 - \lambda) \hat{T}_{\kappa} \] with $\lambda \in [0, 1]$, the smoothing factor.
  • With $\lambda = 1$: "naive" learning; with $\lambda = 0$: arithmetic mean.

Let's Try Again

$\lambda = 0.5$

From Simple to Complex Powerful

Supply: Large Road Network

  • Road network can be an arbitrary graph of nodes (intersections) and edges (road links)
  • 1 bottleneck and 1 travel-time function for each edge
  • Routing algorithm (Contraction Hierarchies) used to compute the travel-time function at the origin-destination level
  • Route choice: the fastest route is selected

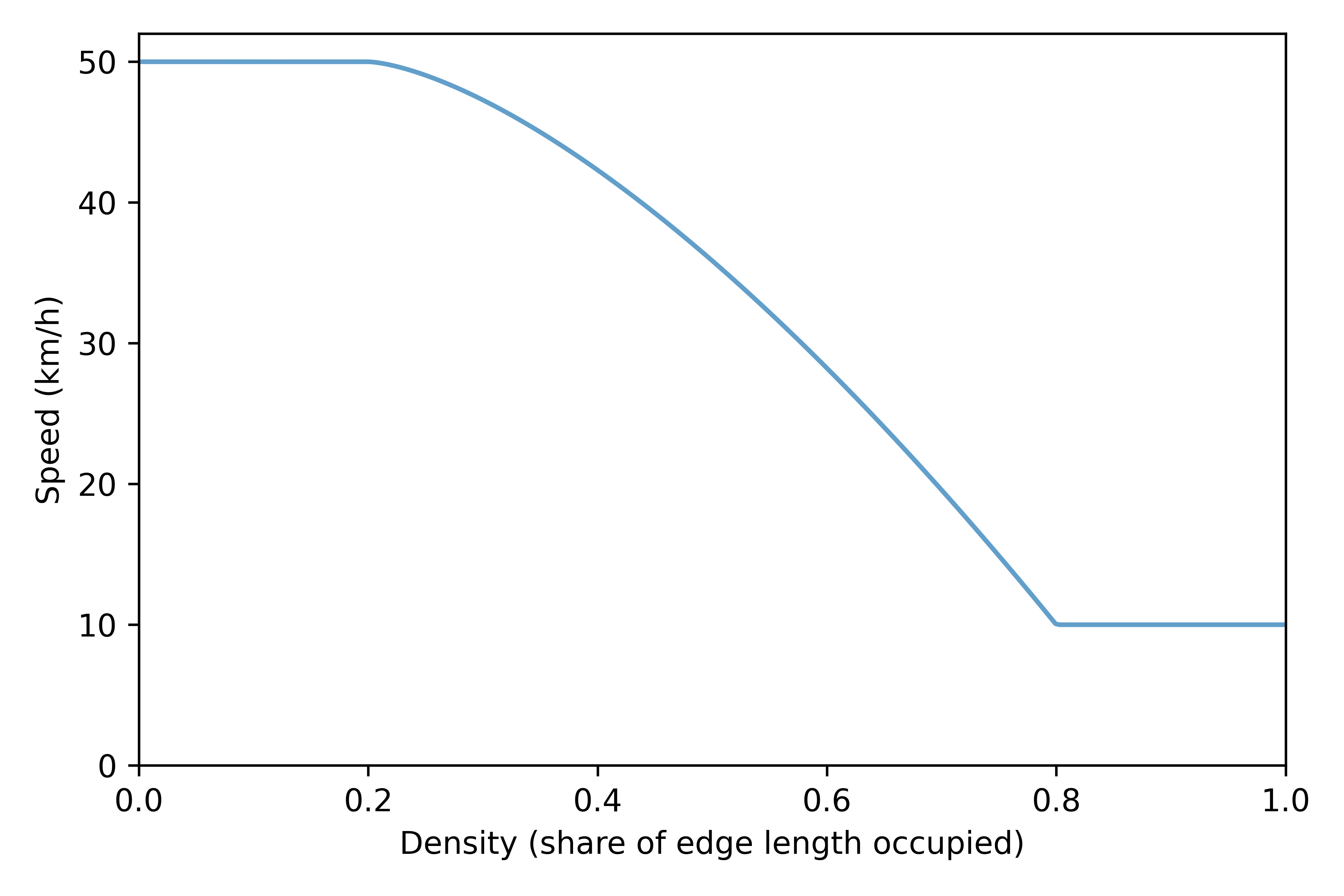
Supply: Congestion Modeling

  • Speed-density function: the speed at which a vehicle travel on the road depends on the density of vehicle currently on the road
  • Bottlenecks: both the inflow and outflow of a link can be limited by the bottleneck's capacity
  • Queue propagation (spillback): Vehicles cannot enter a link if there is no room left; queues propagate backward at a given speed

Supply: Different Vehicle Types

  • Different vehicle headways and passenger car equivalents
  • Different speeds / speed limits
  • Different road access / road restrictions

Demand

  • At the top level, agents choose among an arbitrary number of travel alternatives
  • An alternative is defined as a sequence of trips and a utility function specification
  • Two types of trips: road and virtual
  • The utility of an alternative is a function of:
    • the travel time of each trip
    • the total travel time for all the trips
    • the departure time from the origin of the first trip
    • the arrival time at destination of each trip
  • Choice models:
    • Alternative choice: Multinomial Logit or Deterministic
    • Departure-time choice: Continuous Logit or Multinomial Logit
    • Almost any discrete-choice model is feasible by drawing the epsilon values (idiosyncratic chocs) "offline" and specifying them in the utility

Getting Started with METROPOLIS2

The METROPOLIS2 Website

https://metropolis.lucasjavaudin.com

Running METROPOLIS2 (the Easy Way, on Windows)

  1. Download the last GUI version of METROPOLIS2 for Windows (tab Download on the website).
  2. Execute the .msi file and follow the procedure to install METROPOLIS2 (accept the non-existent risks if the antivirus complains).
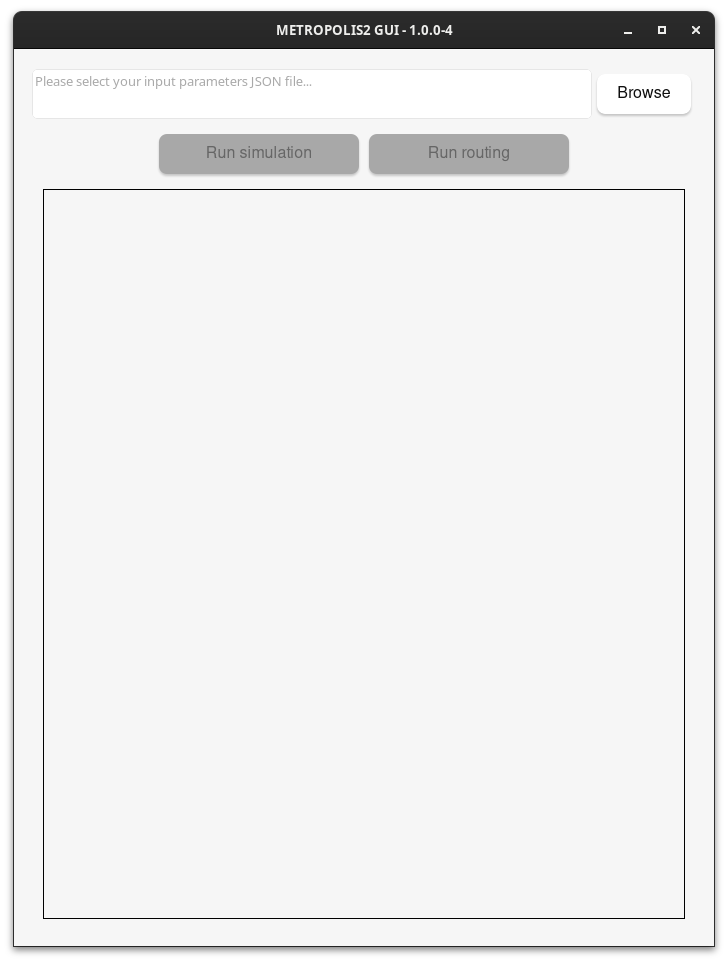
  3. Run the METROPOLIS2 program that is now installed on your computer.
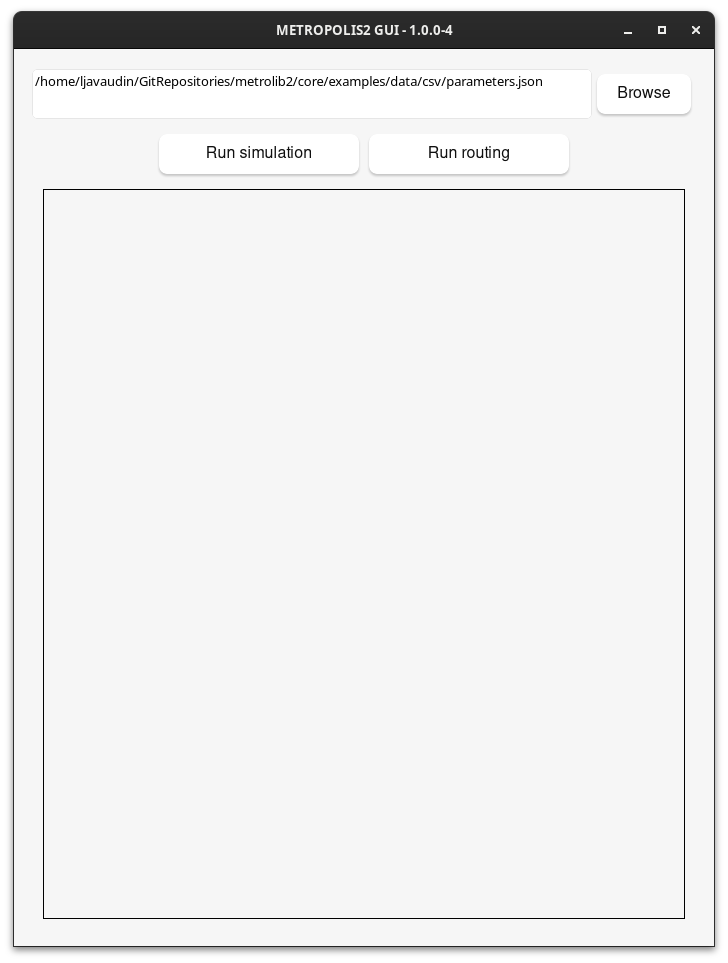
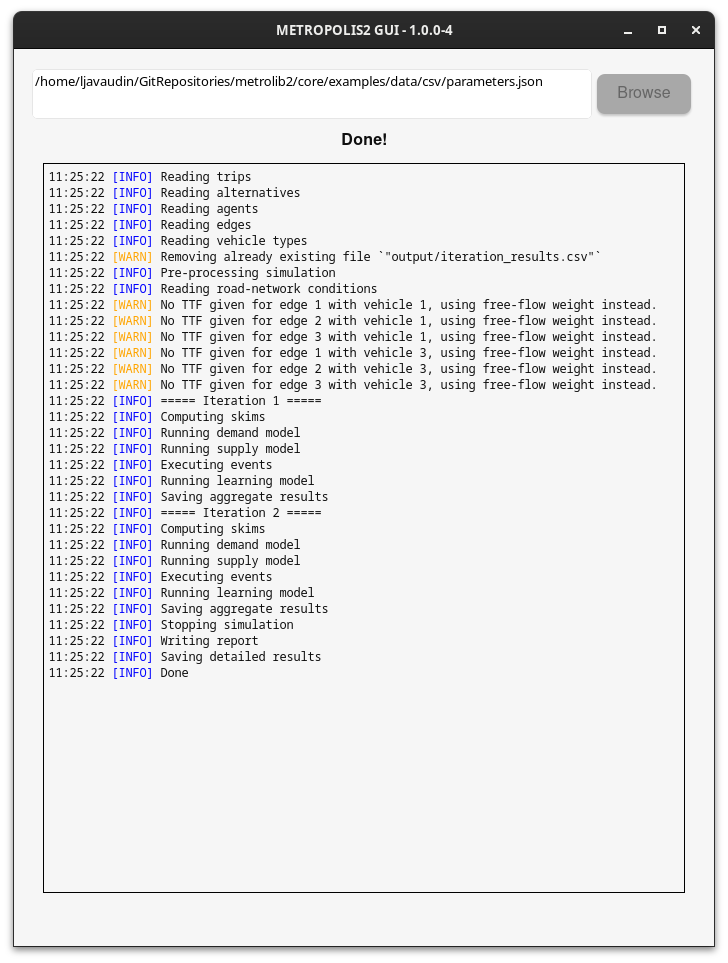
  4. Click on Browse and select your parameters.json file.
  5. Click on the Run simulation button.
  6. Check the logs and close the window when you are done.

Running METROPOLIS2 (the Hard Way)

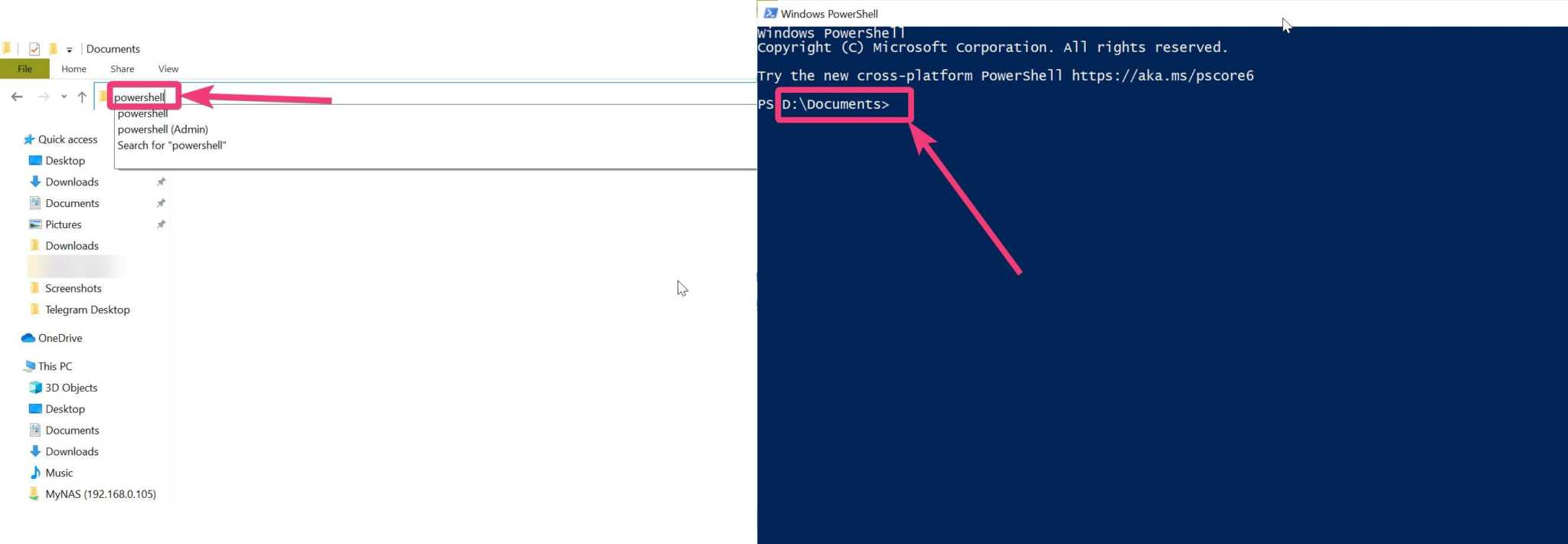
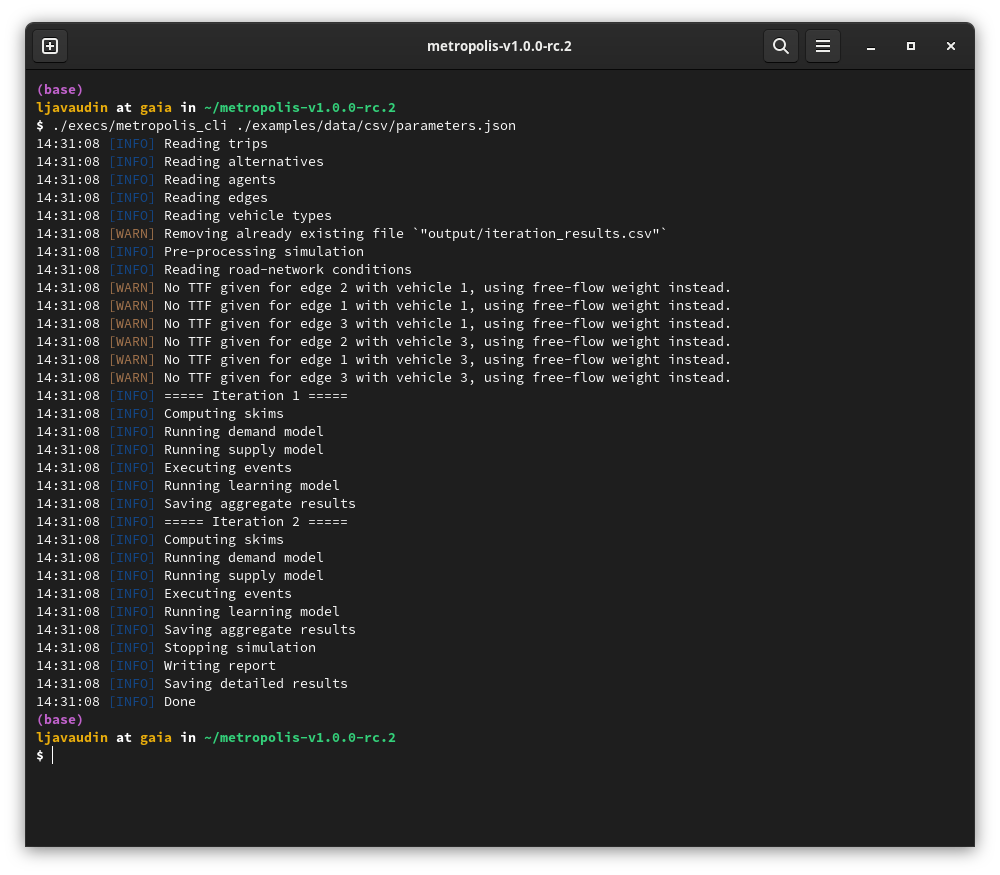
  • Open a Command prompt / Terminal / Powershell with the working directory set to the location of the unzipped directory
  • For Windows, run: 
    
						.\execs\metropolis_cli.exe .\examples\data\csv\parameters.json
  • For MacOS or Linux, run: 
    
						./execs/metropolis_cli ./examples/data/csv/parameters.json
  • Check that the run succeeded
  • The results are stored in examples/data/csv/output/

Files Format: JSON

  • Collection of key-value pairs that can be nested indefinitely 
    
							{
								"key": "value",
								"integer": 1,
								"float": 3.6,
								"boolean": true,
								"array": [
									0, 1, 2
								],
								"nested_array": [
									{"some": "value"},
									{"another": "value"}
								]
							}
  • Very close to Python's dict type
  • Format used to configure the parameters of a METROPOLIS2 simulation and for some output files
  • Syntax definition: https://en.wikipedia.org/wiki/JSON#Syntax

Files Format: CSV

  • Row-oriented file format for tabular data
  • Human readable
  • Compatible with many tools and languages (including Excel!)
  • Used in METROPOLIS2 for most input and output files (comma separator only)
  • Recommended only for small-scale simulations, especially when using Excel
Example of CSV file: 

						col1,col2,col3,col4
						1,Alice,3.2,true
						2,Bob,1.4,false
						3,Charlie,2.5,false

Files Format: Parquet

  • Column-oriented file format for tabular data
  • Binary file (= non human-readable)
  • Built-in compression: smaller file size than CSV
  • Very fast
  • Compatible with Python (polars or pandas libraries) and R (arrow package)
  • Used in METROPOLIS2 for most input and output files
  • Recommended format for large-scale simulations and people working with R or Python

						import polars as pl

						df = pl.DataFrame(
								{
										"agent_id": [0, 1, 2],
										"alt_choice.type": ["Deterministic", "Logit", "Logit"],
										"alt_choice.u": [0.3, 0.6, 0.5],
										"alt_choice.mu": [None, 0.9, 1.0],
										"alt_choice.constants": [[0.9, 1.3, 2.1], None, None],
								}
						)
						df.write_parquet("input/agents.parquet")
						

						In [3]: df
						Out[3]:
						shape: (3, 5)
						┌──────────┬─────────────────┬──────────────┬───────────────┬──────────────────────┐
						│ agent_id ┆ alt_choice.type ┆ alt_choice.u ┆ alt_choice.mu ┆ alt_choice.constants │
						│ ---      ┆ ---             ┆ ---          ┆ ---           ┆ ---                  │
						│ i64      ┆ str             ┆ f64          ┆ f64           ┆ list[f64]            │
						╞══════════╪═════════════════╪══════════════╪═══════════════╪══════════════════════╡
						│ 0        ┆ Deterministic   ┆ 0.3          ┆ null          ┆ [0.9, 1.3, 2.1]      │
						│ 1        ┆ Logit           ┆ 0.6          ┆ 0.9           ┆ null                 │
						│ 2        ┆ Logit           ┆ 0.5          ┆ 1.0           ┆ null                 │
						└──────────┴─────────────────┴──────────────┴───────────────┴──────────────────────┘

METROPOLIS2 Input Files

  • Parameters (JSON)
  • Supply side:
    • Road network (Parquet or CSV)
    • Vehicle types (Parquet or CSV)
  • Demand side:
    • Agents (Parquet or CSV)
    • Travel alternatives (Parquet or CSV)
    • Trips (Parquet or CSV)
  • Optional road-network conditions (Parquet or CSV)

METROPOLIS2 Output Files

  • HTML summary
  • Aggregated results by iteration
  • Supply side:
    • Link-level time-dependent travel times (simulated, expected for last iteration and expected for next iteration)
    • OD-level time-dependent travel times (expected for last iteration)
  • Demand side:
    • Agent-level results
    • Trip-level results
    • Routes taken

Units

For consistency and to prevent mistakes, METROPOLIS2 uses the same units for all input and output variables.

Type Unit Example
Time of day Seconds after midnight 8 * 3600 = 28800 is 8 a.m.
Time duration Seconds 300 (5 minutes)
Length Meters
Speed Meters / Second 50 / 3.6 = 13.89 m/s is 50 km/h
Passenger Car Equivalent (PCE) N/A Usually normalized to 1 for car
Flow PCE / Second 0.5 PCE/s = 1800 PCE per hour
Utility No specific unit (can be monetary units)
Value of Time Utility / Second 15 / 3600 = 0.004167 is 15 $/h

Mistakes are still possibles, be careful!

Documentation

The documentation (WIP) is the best way to understand the input and output formats

https://docs.metropolis.lucasjavaudin.com

Reporting Issues

  • Despite all our efforts, various issues can arise when using METROPOLIS2: e.g., errors when running the simulator or Python scripts, simulator panics, unclear documentation
  • All issues are collected to a centralized place so that users can learn from each other
  • If you face any problem, you should open an issue on this centralized place
  • The issue tracker is hosted on Github: https://github.com/Metropolis2/MetropolisExamples/issues

Task for Next Session

Session 1 Task

  1. Download METROPOLIS2 on the website and check that it runs correctly on your computer by running the example simulation (See First Run slide)
  2. Go through the reference working paper:

    Javaudin, L., & de Palma, A. (2024). METROPOLIS2: Bridging Theory and Simulation in Agent-Based Transport Modeling. THEMA, CY Cergy Paris Université.

  3. Go back to the slides of this session so that you have a global understanding of METROPOLIS2